Repré­sen­ta­tion de données

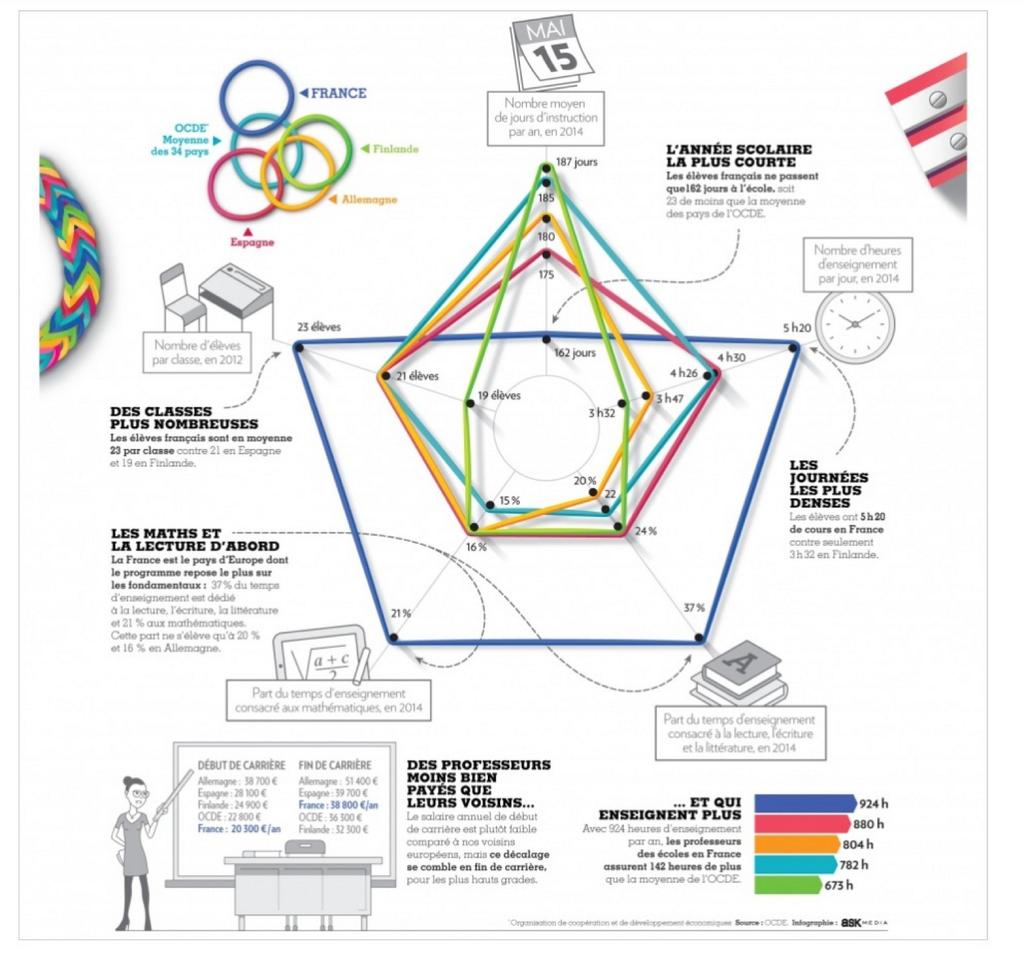
Un graphique tourne un peu avec des données sur l’édu­ca­tion en France :

Les chiffres sont inté­res­sants mais la visua­li­sa­tion est tota­le­ment biai­sée. Le point le plus flagrant est la posi­tion du zéro sur chaque axe qui augmente des diffé­rences.

Première tenta­tive

Quelqu’un a genti­ment fourni une version alter­na­tive, mais tout aussi biai­sée :

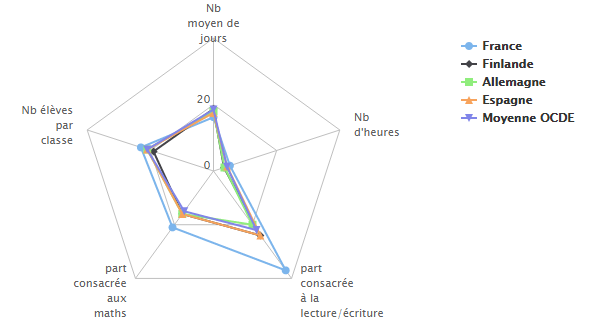
L’in­ten­tion est honnête, mais la volonté de graduer tous les axes sur la même échelle n’a aucun sens quand on compare des choux et des carottes. Ici non seule­ment les données n’ont pas le même sens (le nombre d’heures et le nombre de jours n’ont pas à être compa­rés sur la même échelle, car ils ne repré­sentent pas une donnée cohé­rente), mais elles n’ont même pas la même unités : il y a des heures, des pour­cen­tages, des nombres de jours et des nombres de personnes. Penser que 100% corres­pond à 100 jours et 100 élèves n’a stric­te­ment aucun sens. Du coup les axes sont écra­sés et on ne verrait aucune diffé­rence quand bien même elle serait signi­fi­ca­tive.

Choi­sir sa réfé­rence

Refai­sons donc avec un maxi­mum diffé­rent sur chaque axe, mais lequel ?

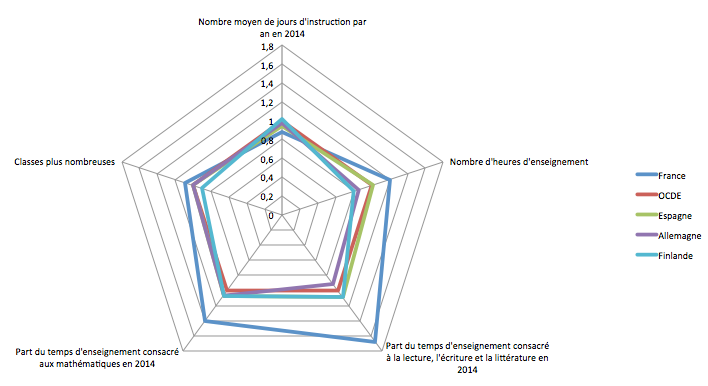
Premier choix, si on tente de compa­rer des chiffres bruts pour voir la répar­ti­tion sur toute la dyna­mique. Ca permet de voir où se massent la plupart des pays, et éven­tuel­le­ment sur quelle dyna­mique ça se répar­tit. On a l’avan­tage aussi d’avoir des chiffres abso­lus et pas des % par rapport à quelqu’un d’autre.

Second choix, on veut avoir une vision de la répar­ti­tion euro­péenne, on les compare donc à la moyenne OCDE (on aurait pu choi­sir la médiane, mais elle ne faisait pas partie des données sources). Ça permet de visua­li­ser faci­le­ment qui s’échappe de la masse.

Dernière possi­bi­lité, si on souhaite compa­rer le reste des pays à la France, on utilise nos propres chiffres comme réfé­rence au lieu de la moyenne OCDE. Ca permet de visua­li­ser plus faci­le­ment où la France parti­cu­liè­re­ment est signi­fi­ca­ti­ve­ment diffé­rente du reste :

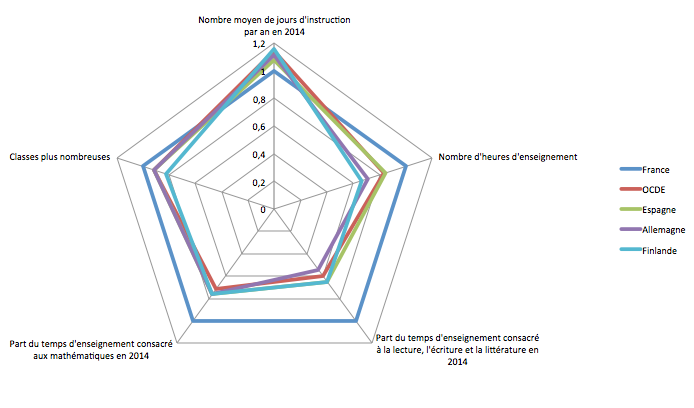 Le choix entre ces trois visua­li­sa­tions est tota­le­ment arbi­traire, en fonc­tion de ce qu’on recherche ou de ce qu’on veut montrer. Dans tous les cas, le choix même de la repré­sen­ta­tion, est déjà un acte d’ana­lyse et donc subjec­tif. Aucune n’est plus « objec­tive » que les autres.

Dans l’in­ten­tion du graphique initial, c’est proba­ble­ment la dernière visua­li­sa­tion qui est la plus perti­nente, vu qu’elle montre faci­le­ment là où la France est isolée.

Toujours aussi biaisé

D’ailleurs mes trois graphiques sont eux-même biai­sés. Le départ à zéro semble natu­rel mais ne l’est en fait pas du tout. Une diffé­rence de 1% pour­rait très bien être extrê­me­ment signi­fi­ca­tive sur une donnée, et ne pas du tout être visible si on graphe bête­ment avec une échelle qui part de zéro.

Même après avoir résolu cette ques­tion des axes, on n’au­rait pas fini pour autant :

Pourquoi unique­ment ces quelques pays, ont-ils été sélec­tion­nés pour accen­tuer un discours pré-établi ? Est-ce qu’on n’au­rait pas plein d’autres pays qui sont proches de nous, voire encore plus diver­gents ?

À défaut de mettre tous les pays de l’OCDE, colo­rier l’écart type serait appré­ciable pour voir si notre écart est parti­cu­liè­re­ment anor­mal ou pas. Avoir la médiane plutôt que la moyenne pour­rait aussi être perti­nent au cas où certains pays sont excep­tion­nel­le­ment hauts ou excep­tion­nel­le­ment bas.

Au niveau des données elles-mêmes, pourquoi avoir pris un pour­cen­tage d’heures de math sur la tota­lité et pas avoir compté le nombre d’heures d’en­sei­gne­ment en valeur absolu ? Au niveau des résul­tats pour l’élève ça aurait été plus cohé­rent.

On a aussi le nombre d’heures par jour et le nombre de jours. Le nombre d’heures par an est-il simi­laire pour tous ? Ca aurait été sacré­ment inté­res­sant de le grapher.

Même chose pour le nombre d’élèves par classe : Pour combien d’en­sei­gnant ? Il y a-t-il des aides, des assis­tants mater­nelles, des assis­tants de vie, des accom­pa­gne­ments person­na­li­sés en plus de l’ins­ti­tu­teur prin­ci­pal ? Quelle est la propor­tion des ensei­gne­ments en demi groupe ou en groupes auto­nomes restreints par rapport aux ensei­gne­ments « pleine classe » ?

Subjec­ti­vité et inten­tion

Vous voulez une repré­sen­ta­tion objec­tive ? Ça n’existe pas. Une donnée objec­tive non plus d’ailleurs, même si ça ressemble à un chiffre brut. C’est bien tout le travail des analystes : Choi­sir une donnée, la méthode de calcul et de récolte, une repré­sen­ta­tion, puis la mettre en forme accom­pa­gnée des expli­ca­tions utiles. Tout ça se fait en fonc­tion d’un objec­tif parti­cu­lier déter­miné au départ.

Du coup le graphique initial est tota­le­ment biaisé, mais fina­le­ment… pas forcé­ment plus qu’un autre. S’il cherche unique­ment à montrer que nous sommes hors du groupe formé par les 4 autres réfé­rences poin­tées, il y réus­sit et proba­ble­ment avec la meilleure visua­li­sa­tion de tout ce qui est présenté ici. Le défaut vient peut être unique­ment de ceux qui le critiquent, qui tentent de le sur-inter­pré­ter.

Il y manquait surtout une légende pour guider la lecture. Ca passait pour des chiffres bruts, ce que ça n’était évidem­ment pas puisqu’il y avait une mise en forme et un objec­tif de commu­ni­ca­tion.