
Rien de plus louche qu’un redécoupage électoral fait en sous-marin, surtout quand il s’accompagne d’un changement de fonctionnement du scrutin.
Vous pouvez être certains qu’il y a une exploitation intensive du paradoxe de Simpson.

Le paradoxe de Simpson c’est profiter d’un découpage des échantillons pour détourner le résultat d’un vote.
Un petit exemple graphique vaut mille discours. On part donc d’un territoire avec 37 votants, 16 bleus et 19 rouges, répartis sans disproportion excessive.
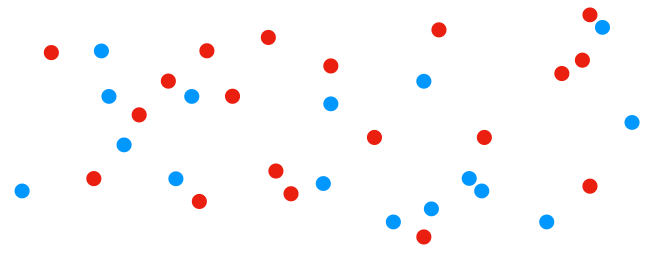
Forcément, sur une élection on se dit que les rouges vont gagner, non ?
Avec une élection purement proportionnelle sur tout le territoire, ce serait le cas. Imaginons qu’on veuille désigner une assemblée de plusieurs élus. Pour qu’elle représente à la fois les électeurs et les régions des électeurs, on choisit de découper le territoire en 3 régions et d’élire un représentant par région.
Imaginez que c’est un partisan des bleus qui fasse le découpage. Que croyez-vous qu’il puisse arriver ?
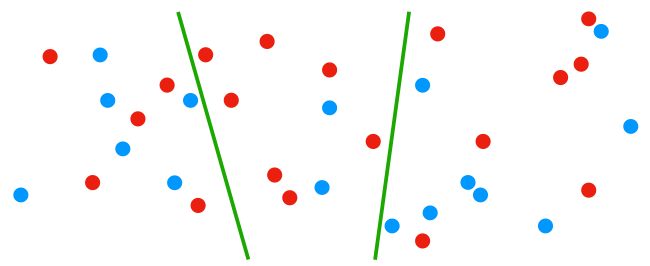
Oui, 2 régions aux bleus, une région aux rouge.
Si l’assemblée fonctionne elle-même à la proportionnelle, les bleus ont le pouvoir de tout décider seuls alors qu’ils sont théoriquement minoritaire.
Dérangeant n’est-ce pas ? Et pourtant, ce mode d’élection ne vous rappelle-t-il rien ?

Un autre arrangement aurait pu attribuer la totalité des représentants aux rouges, laissant les bleus sans aucun représentant.
La seule différence tient à qui fait le découpage.
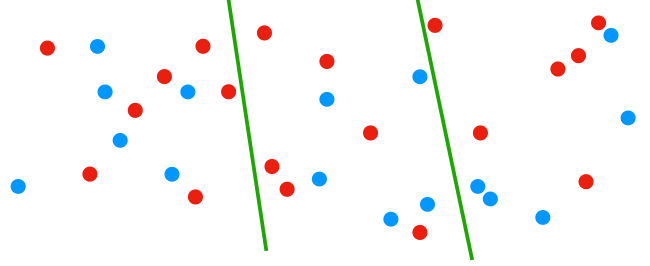
Ne croyez pas que les exemples soient grossiers et tirés par les cheveux. Nos circonscriptions électorales sont bien plus tordues que mes simples lignes droites, et leur composition bien moins homogène que mon exemple.
Un système à deux tours ouvre encore plus de possibilités de manipulation. Si ça vous amuse vous pouvez mettre des rouges clairs et rouges foncés, des bleus clairs et bleus foncés pour représenter les divisions au sein de chaque couleur. Clairs et foncés voteront chacun pour eux au premier tour mais se rassembleront au second tour.
Au final c’est juste un jeu savant à base d’énormes grilles de chiffres mais qui peut se biaiser bien plus fortement que mon simple exemple ne le laisse croire.

Évidemment chaque redécoupage sera publiquement motivé par des questions démographiques, des questions de représentation de territoire, des équilibre ville/campagne, etc. En réalité les critères, leur pondération et la façon dont on les prend en compte resteront guidé par nos tableaux de chiffres et le paradoxe de Simpson.
Au mieux on peut avoir des accords entre les plus grandes forces en présence en fonction de leur propre poids dans le bras de fer du moment et de leurs espoirs pour le futur.
TL;DR: Le découpage électoral ne fait que révéler le choix de celui qui découpe. Le système majoritaire à deux tours ne fait que lui faciliter le travail.
Laisser un commentaire